Fertilizer management and plant nutrients

Using less fertilizer in the field

Japan relies on imports for most of the raw materials needed to make chemical fertilizers, but organic fertilizers are also being reconsidered. The shift from chemical to organic fertilizers has been caused not only by international price fluctuations, but also by the rising cost of electricity required for the industrial production of chemical fertilizers, increased transportation and other expenses, and the environmental impact of fertilizer production. First, Japan imports almost all of the phosphorus ore and karate chloride it uses, but since these resources are unevenly distributed around the world, it means the import partners are unevenly distributed as well. For example, China and Jordan are sources for phosphorus ore, the U.S. and China are good sources for phosphorus, and Canada exports karate chloride. The price dominance of these raw material supplier countries is extremely high. Second, many chemical nitrogen fertilizers are produced industrially using the Haber-Bosch method, which is a scientific fixation of airborne nitrogen. Natural gas is used in large quantities for this process, both as a source of hydrogen and as a power source for creating high temperatures and pressure. The high price of this natural gas makes it difficult to obtain a stable supply. Third, large amounts of energy are used in fertilizer production, which can produce large amounts of carbon dioxide. Nitrogen oxides are also a concern for air and ocean pollution and other negative effects; for example, in the Gulf of Mexico, fertilizer runoff has created a dead zone where oxygen is absent and marine life is unable to thrive. Furthermore, marine nitrogen is converted to dinitrogen monoxide, which has a stronger warming effect than carbon dioxide as a greenhouse gas. Thus, chemical fertilizers are manufactured using fossil resources, such oil and other fossil fuels. This, in turn, is associated with resource depletion and negative environmental impacts, making it a global environmental issue.

It is important to adjust the amount of fertilizer used, not only for the sake of the global environment, but also for the good of farmland and agricultural products. For example, the amount of basal fertilizer should be varied according to cucumber variety and its soil quality. Cucumbers are harvested before ripening, so they require less fertilizer, in terms of yield, than tomatoes, which are harvested when fully ripe. However, cucumber crops are heavily fertilized in Japan. Some JAs recommend applying 50–60 kg of nitrogen as a base fertilizer. Using so much fertilizer at once is often too much. The Fertilizer Dealer’s Handbook clearly states that additional fertilizer should be applied at a ratio of 1 kg of nitrogen for every 100 kg of cucumber yield. This is an outrageous amount. The day after the fertilizer is applied, the fruit is bent and tapered.

The long-term accumulation of fertilizer nutrients in the soil is progressing, due to the heavy application of fertilizers, pesticides, and organic materials, and physiological nutrient disorders due to excessive crop elements are frequent in many areas of production. In order for crops to grow normally, the nutrient status of the soil should be adjusted to the amount required by the crop and balanced with other components. Fertilization should be used as a supplement when there is a deficiency and withheld in farmlands with surplus ingredients.

Long-term diagnoses, fertilizer application, and homegrown fertilizers

The important thing about taking advantage of soil diagnosis is not to be overwhelmed by the results of a single diagnosis, but rather to look at the figures over a span of several years. For example, when you try to lower a pH that is too high, it is possible to lower it within 1 year if you use diluted sulfuric acid or sulfur, but the crop growth will be worse. If there is a lot of potassium in the field and you want to reduce it, it is a good idea not to stop fertilizing in the first year, but instead to begin by reducing fertilization by half. As is the case with human beings, fields are living things, and sudden changes are unreasonable and will lead to many problems.

Even if you choose to use the same fertilizer as in the past, its cost can be reduced by changing the application method. If you change the application method only in the ridges, or around the roots of the crop, to a local application method, the absorption efficiency will increase. In extreme cases, the amount of fertilizer can be cut in half if new application methods are devised. A machine is needed to use this fertilization method in field crops. In a vinyl house, a control machine can be used to apply ditch fertilizer under the beds. Hydroponic and soil culture is the ultimate application form, as it fertilizes only around the roots using irrigation tubes and liquid fertilizer in amounts as and when needed, based on a growth assessment.

The switch from chemical to organic fertilizers has many benefits, partly due to increased costs of chemical fertilizers in Japan. It has been reported that the traditional farming method of converting animal wastes into humus via microorganisms is resistant to pests and diseases and does not show any decrease in crop yields for a long time. Soil humus provides a good habitat for fungi and promotes the growth of the plant’s root system. This causes the plants, especially fruit and tea trees, to spread their roots deep into the ground, to send out healthy leaves, and to have good branches. The squeezed husks of straw and sugar cane can later become the bedding for livestock, such as chickens and cows, and then mixed with human waste and returned to the fields to produce agricultural products. Traditional farming knows that these animal and plant wastes are the heart of the fertilization cycle.

In addition, there are local raw materials for some kinds of fertilizer available free of charge. There are many things that cannot be used as they are, but they can be mixed and put into beds, such as soybean meal, trash wheat, rice bran, eggshells, shells, pruning branches, roadside grasses, or chestnut or leek peels. There’s also a lot of food waste in urban areas. There are ways to use the phosphoric acid that has accumulated in the field with the chemical fertilizers that have already been applied by changing the form of the phosphoric acid, such as planting other plants where mycorrhizal fungi have emerged, or promoting fermentation with microorganisms. In recent years, a variety of farming methods have been advocated and demonstrated, including natural farming, carbon farming, and Synecoculture^TM. We will continue to introduce examples of the use of each fertilizer and farming method in the future, so we encourage readers to look for materials that are familiar.

A chemical understanding of fertilizer

First of all, it is necessary to diagnose the soil properly and to stop unnecessary fertilization. A general soil diagnosis considers nine soil nutrition elements: pH, electrical conductivity (EC), Cation exchange capacity (CEC), available phosphoric acid, exchangeable potash, exchangeable lime, exchangeable magnesium oxide, and nitrate. There are 17 known elements that are essential for crop growth. Of these, those that require relatively large amounts are called “macronutrients,” while those that require only a small amount are called “micronutrients.”  

Of these elements, carbon is supplied by carbon dioxide in the air, and oxygen and hydrogen are mainly supplied via water through the plant’s roots. Of course, some oxygen is also taken from carbon dioxide. These nutrients, with the exception of hydrogen, oxygen, and carbon, often require artificial supplementation. They are absorbed and used from the soil in their inorganic form; however, if the soil chemistry deteriorates, crops will not be able to take in the right amount of necessary nutrients, and their growth will be poor. Eventually, symptoms of nutrient deficiency-specific disorders appear on the leaves, stems, cotyledons, roots, etc., and elemental disorders (i.e., nutritional disorders) appear.

Ch. 1 Essential crop nutrients

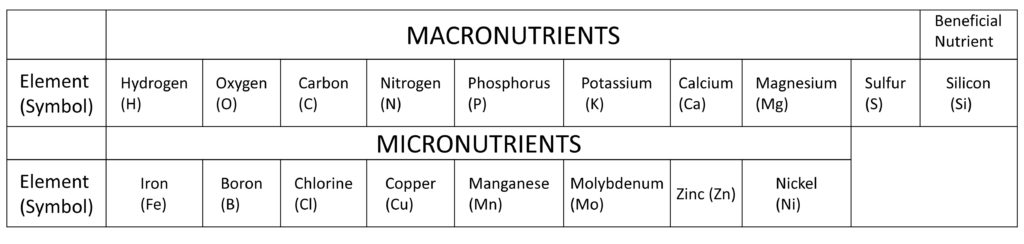
In addition, some components that are not considered essential elements for crops, such as silicon, are highly demanded in some crops and follow the essential elements. Silicone is a useful element for paddy rice because a lack of silicone causes poor growth.

In very small parts of the soil, clay minerals and humus combine to form clay–humus complexes. We usually call this a “soil colloid.” A soil colloid has a negative (-) charge on its surface and adsorbs and retains fertilizer components such as calcium, magnesium, potassium, and sodium with a positive (+) charge. Small grains with ions that are positively charged are called “cations,” and those that are negatively charged are called “anions.” Considering these ions of fertilizer, for example, ammonium sulfate (NH₄SO₄) is divided into +1 ammonium ion and -2 sulfate ions when dissolved in water. Of these, the ammonium ions of the particles with positive charge are electrostatically adsorbed by the colloids of the soil (i.e., the particles with negative charge). This reaction allows the fertilizer, ammonia, to be retained in the soil.

A fertilizer component that has a positive charge is called a “base,” and the phenomenon of being adsorbed by soil particles that have a negative charge is called “base adsorption.” Because of this function in the soil, it is neither washed away by fertilizer or water nor causes a concentration problem, even when applied in a certain amount. Cations other than hydrogen ions are called “exchangeable bases” among the cations that are adsorbed by the soil colloid and are easily replaced by other cations. Since exchangeable bases are most easily absorbed and utilized by crops, soils containing large amounts of exchangeable bases are generally said to be more fertile and to have a stronger ability to absorb and retain fertilizer components such as ammonia. Micronutrients are also adsorbed by this soil colloid.